Định lý 3 đường vuông góc là gì? Phương pháp chứng minh Định lý 3 đường vuông góc? Định hướng phương pháp hình thành và phát triển môn toán?

Nội dung chính

• Định lý 3 đường vuông góc là gì? Phương pháp chứng minh Định lý 3 đường vuông góc?
• Nhận biết khái niệm đường vuông góc là yêu cầu cần đạt trong chương trình toán lớp mấy?
• Định hướng phương pháp hình thành và phát triển các phẩm chất chủ yếu và năng lực chung môn toán?

Định lý 3 đường vuông góc là gì? Phương pháp chứng minh Định lý 3 đường vuông góc?

Định lý 3 đường vuông góc: là một khái niệm quan trọng trong hình học không gian, được phát triển bởi Euclid. Định lý này giúp xác định mối quan hệ vuông góc giữa các đường thẳng và mặt phẳng trong không gian ba chiều.

Định lý nêu rằng:

Phương pháp chứng minh Định lý 3 đường vuông góc?

Định lý 3 đường vuông góc, được phát triển bởi Euclid, là một trong những định lý cơ bản trong hình học Euclid. Dưới đây là các bước để chứng minh định lý này, áp dụng các khái niệm và phương pháp hình học cổ điển.

Bước 1: Xác định điều kiện ban đầu. Giả sử có hai đường thẳng AB và AC không trùng nhau và nằm trên một mặt phẳng, và một đường thẳng AD không nằm trên mặt phẳng đó.

Bước 2: Vẽ hình chiếu vuông góc của đường thẳng AD lên mặt phẳng chứa AB và AC, gọi là AE. Để chứng minh AD vuông góc với mặt phẳng, ta cần chứng minh AE vuông góc với cả AB và AC.

Bước 3: Sử dụng các định nghĩa và tính chất cơ bản của hình học, như tính chất của đường vuông góc và các góc tạo bởi các đường thẳng, để chứng minh AE vuông góc với AB và AC. Điều này bao gồm chứng minh rằng các góc tạo bởi AE và AB, cũng như AE và AC, đều là góc vuông.

Bước 4: Áp dụng các quy tắc đồng nhất, cộng, và quy tắc trừ để khẳng định rằng nếu AE vuông góc với AB và AC, thì AD phải vuông góc với mặt phẳng chứa AB và AC.

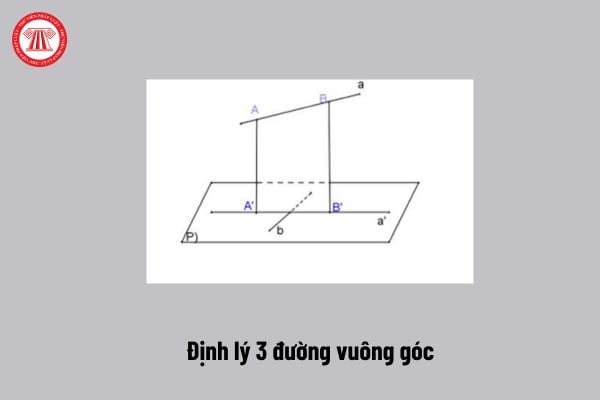
Định lý 3 đường vuông góc là gì? (Hình từ Internet)

Nhận biết khái niệm đường vuông góc là yêu cầu cần đạt trong chương trình toán lớp mấy?

Căn cứ tại tiểu mục 2 mục V chương trình giáo dục phổ thông ôn toán Ban hành kèm theo Thông tư 32/2018/TT-BGDĐT quy định như sau:

Theo đó, nhận biết được khái niệm đường vuông góc là yêu cầu cần đạt của nội dung trong phần hình học phẳng ở chương trình Toán lớp 7.

Định hướng phương pháp hình thành và phát triển các phẩm chất chủ yếu và năng lực chung môn toán?

Căn cứ theo tiểu mục 2 mục VI chương trình giáo dục phổ thông môn toán ban hành kèm theo Thông tư 32/2018/TT-BGDĐT quy Định hướng phương pháp hình thành và phát triển các phẩm chất chủ yếu và năng lực chung như sau:

(1) Phương pháp hình thành, phát triển các phẩm chất chủ yếu:

Thông qua việc tổ chức các hoạt động học tập, môn Toán góp phần cùng các môn học và hoạt động giáo dục khác giúp học sinh rèn luyện tính trung thực, tình yêu lao động, tinh thần trách nhiệm, ý thức hoàn thành nhiệm vụ học tập; bồi dưỡng sự tự tin, hứng thú học tập, thói quen đọc sách và ý thức tìm tòi, khám phá khoa học.

(2) Phương pháp hình thành, phát triển các năng lực chung:

- Môn Toán góp phần hình thành và phát triển năng lực tự chủ và tự học thông qua việc rèn luyện cho người học biết cách lựa chọn mục tiêu, lập được kế hoạch học tập, hình thành cách tự học, rút kinh nghiệm và điều chỉnh để có thể vận dụng vào các tình huống khác trong quá trình học các khái niệm, kiến thức và kĩ năng toán học cũng như khi thực hành, luyện tập hoặc tự lực giải toán, giải quyết các vấn đề có ý nghĩa toán học.

- Môn Toán góp phần hình thành và phát triển năng lực giao tiếp và hợp tác thông qua việc nghe hiểu, đọc hiểu, ghi chép, diễn tả được các thông tin toán học cần thiết trong văn bản toán học; thông qua sử dụng hiệu quả ngôn ngữ toán học kết hợp với ngôn ngữ thông thường để trao đổi, trình bày được các nội dung, ý tưởng, giải pháp toán học trong sự tương tác với người khác, đồng thời thể hiện sự tự tin, tôn trọng người đối thoại khi mô tả, giải thích các nội dung, ý tưởng toán học.

- Môn Toán góp phần hình thành và phát triển năng lực giải quyết vấn đề và sáng tạo thông qua việc giúp học sinh nhận biết được tình huống có vấn đề; chia sẻ sự am hiểu vấn đề với người khác; biết đề xuất, lựa chọn được cách thức, quy trình giải quyết vấn đề và biết trình bày giải pháp cho vấn đề; biết đánh giá giải pháp đã thực hiện và khái quát hoá cho vấn đề tương tự.