Các dạng đồ thị hàm số bậc ba gồm những dạng nào? Câu hỏi ở dạng trắc nghiệm trả lời ngắn môn toán kỳ thi tốt nghiệp THPT là bao nhiêu câu?
- Các dạng đồ thị hàm số bậc ba gồm những dạng nào?
- Những lưu ý khi làm bài tập liên quan đến đồ thị hàm số bậc ba? Câu hỏi ở dạng trắc nghiệm trả lời ngắn môn toán kỳ thi tốt nghiệp THPT là bao nhiêu câu?
- Thí sinh lựa chọn chính xác cả 04 ý trong 01 câu hỏi môn toán kỳ thi tốt nghiệp THPT thì được tính điểm như thế nào?
Các dạng đồ thị hàm số bậc ba gồm những dạng nào?
Hàm số bậc 3 là hàm số có dạng như sau:
y=ax^3+bx^2+cx+d (a≠0)
Được chi làm ba trường hợp cụ thể:
+ Trường hợp 1: Phương trình y'=0 có hai nghiệm phân biệt
Khi phương trình đạo hàm bậc nhất y=ax^3+bx^2+cx+d có hai nghiệm phân biệt, điều này đồng nghĩa với việc đồ thị hàm số bậc ba có hai điểm cực trị (một cực đại và một cực tiểu).
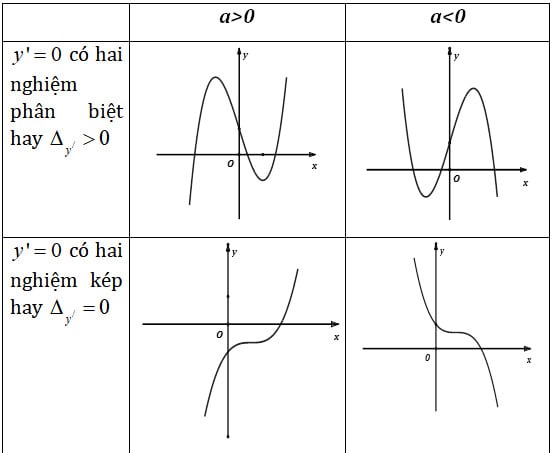
+ Trường hợp 2: Phương trình y'=0 có 1 nghiệm (kép)
Khi phương trình đạo hàm có một nghiệm kép. Đồ thị hàm số bậc ba không có điểm cực trị và tiếp tuyến tại điểm uốn song song với trục hoành.
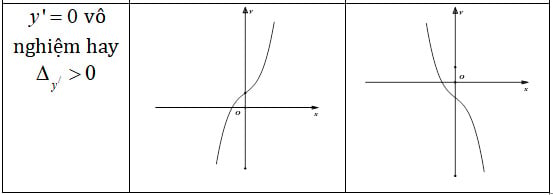
+ Trường hợp 3: Phương trình y'=0 vô nghiệm
Đồ thị hàm số bậc ba cũng không có điểm cực trị nhưng tiếp tuyến tại điểm uốn không song song với trục hoành
*Nội dung trên chỉ mang tình chất tham khảo.

Các dạng đồ thị hàm số bậc ba gồm những dạng nào? Câu hỏi ở dạng trắc nghiệm trả lời ngắn môn toán kỳ thi tốt nghiệp THPT là bao nhiêu câu? (Hình từ Internet)
Những lưu ý khi làm bài tập liên quan đến đồ thị hàm số bậc ba? Câu hỏi ở dạng trắc nghiệm trả lời ngắn môn toán kỳ thi tốt nghiệp THPT là bao nhiêu câu?
Khi giải bài tập liên quan đến đồ thị hàm số bậc ba, cần chú ý các điểm sau để làm bài hiệu quả:
(1) Đọc kỹ yêu cầu bài toán + Xác định yêu cầu: xét tính chất, tìm cực trị, vẽ đồ thị, hay giải phương trình liên quan. + Kiểm tra dạng bài: hàm số tổng quát, bài toán thực tế, hay bài toán liên quan đến bất phương trình. (2) Phân tích hàm số + Dạng hàm số: Đảm bảo nhận diện đúng dạng hàm bậc ba y=ax^3+bx^2+cx+d, với a≠0. + Tính đạo hàm: Tính y′=3ax^2+2bx+c để phân tích tính đơn điệu, tìm cực trị, và xác định điểm uốn. (3) Tìm các yếu tố đặc trưng + Tập xác định: Thường là |R, nhưng cần chú ý các giới hạn nếu bài toán thực tế. + Điểm cực trị: Giải phương trình y′=0 để tìm x tại các điểm cực trị. + Điểm uốn: Xác định y′′=6ax+2b=0 để tìm vị trí điểm uốn. + Đồ thị: Xác định chiều biến thiên, cực trị, điểm uốn, và giao điểm với các trục để phác họa đồ thị. (4) Chú ý cách trình bày + Lập bảng biến thiên: Rõ ràng, chính xác, thể hiện chiều biến thiên (tăng/giảm) và các giá trị đặc biệt như cực trị, điểm uốn. + Vẽ đồ thị hàm số bậc ba: Chú ý các yếu tố chính: giao điểm với trục Ox,Oy, vị trí cực trị, và điểm uốn. Phân biệt trường hợp a>0 (đồ thị tăng cuối cùng) và a<0 (đồ thị giảm cuối cùng). (5) Kiểm tra lại bài làm + Tính toán cẩn thận: Đặc biệt khi giải phương trình đạo hàm y′=0 và đạo hàm cấp hai y′′=0. + Đối chiếu với đồ thị: Đảm bảo đồ thị phù hợp với các tính chất đã tìm được (cực trị, điểm uốn, giao điểm). + Kết luận rõ ràng: Ghi lại kết quả cuối cùng của bài toán, tránh thiếu sót. Tóm lại, khi giải bài đồ thị hàm số bậc ba, trước tiên cần xác định yêu cầu như tìm cực trị, điểm uốn hay vẽ đồ thị. Tính đạo hàm bậc nhất để xét tính đơn điệu, tìm cực trị và đạo hàm bậc hai để xác định điểm uốn. Lập bảng biến thiên, vẽ đồ thị chú ý đến giao điểm với trục, hình dạng (đơn điệu, hình sóng hoặc có điểm uốn). Nếu bài toán thực tế, cần xét thêm điều kiện giới hạn. Đảm bảo đồ thị và kết quả khớp với phân tích, trình bày rõ ràng và kiểm tra lại để tránh sai sót. |
*Nội dung trên chỉ mang tình chất tham khảo.
Căn cứ theo tiểu mục 2 Mục I Phụ lục ban hành kèm theo Quyết định 764/QĐ-BGDĐT năm 2024 quy định về cấu trúc đề thi.
Theo đó, câu hỏi ở dạng trắc nghiệm môn toán kỳ thi tốt nghiệp THPT được quy định gồm 22 câu với nội dung trắc nghiệm nhiều lựa chọn, trắc nghiệm dạng Đúng/Sai, trắc nghiệm dạng trả lời ngắn, cụ thể:
+ Phần 1: 12 câu hỏi ở dạng thức trắc nghiệm nhiều lựa chọn cho 04 phương án chọn 01 đáp án đúng;
+ Phần 2: 04 câu hỏi ở dạng thức trắc nghiệm dạng Đúng/Sai. Mỗi câu hỏi có 04 ý, tại mỗi ý thí sinh lựa chọn đúng hoặc sai;
+ Phần 3: 06 câu hỏi ở dạng thức trắc nghiệm dạng trả lời ngắn. Thí sinh tô vào các ô tương ứng với đáp án của mình.
Như vậy, câu hỏi ở dạng trắc nghiệm trả lời ngắn môn toán kỳ thi tốt nghiệp THPT là 06 câu.
Thí sinh lựa chọn chính xác cả 04 ý trong 01 câu hỏi môn toán kỳ thi tốt nghiệp THPT thì được tính điểm như thế nào?
Căn cứ theo điểm b tiểu mục 2 Mục II Phụ lục ban hành kèm theo Quyết định 764/QĐ-BGDĐT năm 2024 quy định về cách thức tính điểm như sau:
II. Cách thức tính điểm:
1. Tự luận:
a) Phần I - Đọc hiểu: 04 điểm.
b) Phần II - Viết: 06 điểm.
c) Tổng điểm tối đa toàn bài: 10 điểm.
2. Trắc nghiệm:
a) Phần I: Mỗi câu trả lời đúng thí sinh được 0,25 điểm
b) Phần II:
- Thí sinh chỉ lựa chọn chính xác 01 ý trong 01 câu hỏi được 0,1 điểm;
- Thí sinh chỉ lựa chọn chính xác 02 ý trong 01 câu hỏi được 0,25 điểm;
- Thí sinh chỉ lựa chọn chính xác 03 ý trong 01 câu hỏi được 0,5 điểm;
- Thí sinh lựa chọn chính xác cả 04 ý trong 01 câu hỏi được 1 điểm.
c) Phần III:
- Môn Toán: Mỗi câu trả lời đúng thí sinh được 0,5 điểm.
- Các môn khác: Mỗi câu trả lời đúng thí sinh được 0,25 điểm.
d) Tổng điểm tối đa toàn bài: 10 điểm
Theo đó, đối với trưởng hợp thí sinh lựa chọn chính xác cả 04 ý trong 01 câu hỏi thuộc phần II môn toán kỳ thi tốt nghiệp THPT thì được tính là 01 điểm.










Quý khách cần hỏi thêm thông tin về có thể đặt câu hỏi tại đây.
- 5 nguyên tắc kiểm soát ô nhiễm môi trường biển và hải đảo hiện nay? Nội dung kiểm soát gồm những gì?
- Công văn 4370/BTC-DNTN không phải thay đổi đăng ký kinh doanh sau sáp nhập tỉnh xã? Tải về Công văn 4370/BTC-DNTN?
- Lễ Tiệc ly là gì? Lễ Tiệc ly ngày nào? Lễ Tiệc ly có phải lễ trọng không? Lễ Tiệc ly thứ Năm Tuần Thánh có phải ngày lễ lớn của Việt Nam?
- Từ 01/7/2025, bỏ cấp huyện thì 100% biên chế cán bộ công chức huyện bố trí về xã hay lên tỉnh?
- Dự án đầu tư xây dựng sử dụng vốn hỗn hợp gồm dự án nào? Công năng phục vụ có phải căn cứ để phân loại dự án đầu tư xây dựng không?









